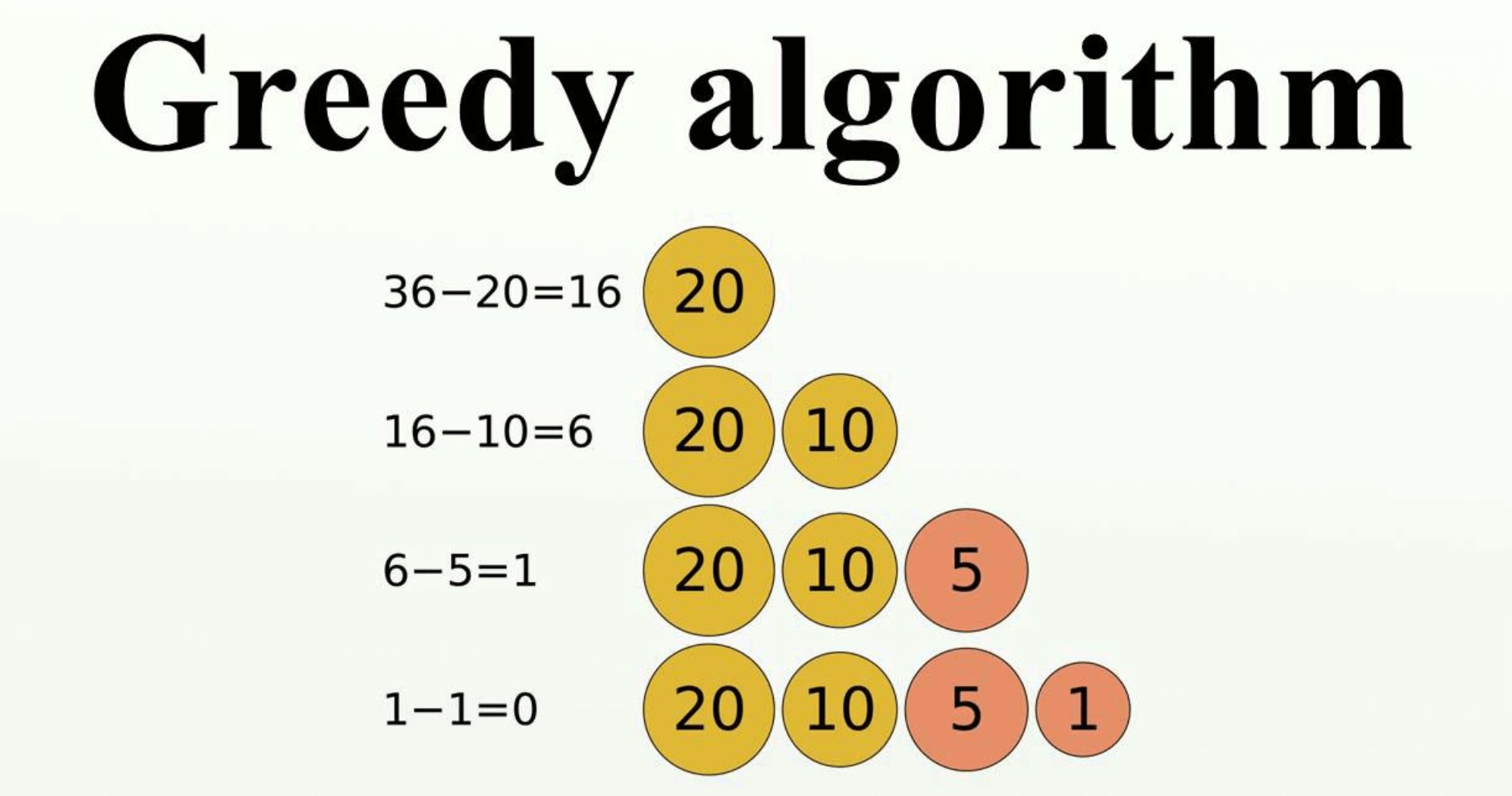
不是对所有问题都得到整体最优解,这种策略必须具备无后效性,它只与当前状态有关。
首先建立数学模型,然后把求解的问题分成若干个小问题,对每个小问题求解,得到子问题的最优解,然后根据子问题的最优解,得到问题的解。
主要思想是局部最优解推出全局最优解,是贪心算法的核心思想。
题目要求: 求一个数组,连续子数组的和最大值,数组中允许有负数。
def max_sub_num_array_sum(num_array):
"""
:param num_array: number array
:return: max sub number array sum
"""
assert isinstance(num_array, (list, tuple))
assert len(num_array) > 0
max_sum = num_array[0]
current_max_sum = num_array[0]
sub_array = [num_array[0]]
for num in num_array[1:]:
current_max_sum += num
sub_array.append(num)
if current_max_sum < 0:
current_max_sum = 0
sub_array = []
if current_max_sum > max_sum:
max_sum = current_max_sum
if max_sum < 0:
max_sum = max(num_array)
sub_array = [max_sum]
print (sub_array)
return max_sum
if __name__ == '__main__':
array = [-1, 1, -3, 4, -1, 2, 1, -5, 4]
print (max_sub_num_array_sum(array))
运行结果
[4, -1, 2, 1, -5, 4]
6
题目要求: 现在为已经站成一排的小朋友分糖果,保证每个小朋友至少有一个糖果,同时保证个子比相邻小朋友高的所分的糖果要比他的邻居多,按照这样的分食方法,最少需要多少糖果。
def dividing_candy(childs_height):
"""
:param childs_height:a list of child height
:return:
Make sure that each child has at least one candy, and that the number of sweets
that are higher than the neighbors is
higher than that of his neighbors. According to this method of feeding,
at least how many candies are needed.
"""
assert len(childs_height) > 0
candies_array = [1] * len(childs_height)
index = 0
last_height = childs_height[0]
for next_height in childs_height[1:]:
if next_height > last_height:
candies_array[index + 1] = candies_array[index] + 1
last_height = next_height
index += 1
candies_array.reverse()
childs_height.reverse()
index = 0
last_height = childs_height[0]
for next_height in childs_height[1:]:
if next_height > last_height and candies_array[index + 1] <= candies_array[index]:
candies_array[index + 1] = candies_array[index] + 1
last_height = next_height
index += 1
candies_array.reverse()
childs_height.reverse()
print (childs_height)
print (candies_array)
candies = sum(candies_array)
return candies
if __name__ == '__main__':
array = [4, 2, 6, 8, 5]
print (dividing_candy(array))
运行结果
[4, 2, 6, 8, 5]
[2, 1, 2, 3, 1]
9
题目要求: 给定一个整数数组,数组中的元素代表在当前位置能够向前跳的最远距离,判断给定的这个跳远策略能否跳到最后的位置。
# -*- coding: utf-8 -*-
__author__ = 'gzp'
def can_jump(jump_array):
"""
:param jump_array:
:return:
Given an array of integers, the elements in the array represent the farthest distance
that can be jumped forward at the current position,
and whether the given long jump strategy can jump to the last position.
"""
if len(jump_array) == 0:
return True
max_jump = jump_array[0]
last_steps = len(jump_array[1:])
for location, jump_num in enumerate(jump_array[1:], start=1):
if max_jump == 0:
return False
max_jump -= 1
if max_jump < jump_num:
max_jump = jump_num
if max_jump + location > last_steps:
return True
return False
if __name__ == '__main__':
array = [2, 3, 1, 1, 0]
print (can_jump(array))
array = [2, 3, 1, 1, 4]
print (can_jump(array))
array = [2, 0, 0, 4, 3]
print (can_jump(array))
运行结果
False
True
False